Ciąg Fibonacciego jest naprawdę ciekawym ciągiem możemy go znaleźć w wielu sytuacjach czy dziedzinach np. w matematyce
lub przy … rozmnażaniu królików. Ciekawostka jest to że liczba płatków w większości kwiatów to właśnie liczby Fibonacciego , większość zwierząt rozmnaża się także zgodnie z ciągiem Fibonacciego.
http://pl.wikipedia.org/wiki/Ciąg_Fibonacciego
Ciąg Fibonacciego jest rekurencyjny tzn. kolejny wyraz jest równy sumie poprzednich dwóch wyrazów co prowadzi do ciekawych właściwości oraz powiązania z innym pojęciem matematycznym który występuje prawie wszędzie nawet w ludzkim ciele 🙂 ! Chodzi oczywiście o Złoty Podział
http://pl.wikipedia.org/wiki/Złoty_podział z tym zaś pojęciem związana jest liczba FI
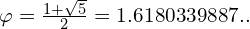
Ciąg wygląda tak
0,1,1,2,3,5,8,13,21,34,55,89,144,..
Przyglądając się ciągowi możemy znaleźć 3 ciekawe właściwości
- Pierwsza z nich jeśli spojrzymy na 3 , 6 i 9 wyraz ciągu zauważymy że wszystkie są podzielne przez 2
następnie patrząc na 4 , 8 i 12 wyraz ciągu wszystkie są podzielne przez 3. Co piąty wyraz dzieli się przez 5 co szósty przez 8 co siódmy przez 13 co ósmy przez 21 i tak dalej. Dzielniki które uzyskaliśmy są kolejnymi liczbami ciągu Fibonacciego 😉
- Druga z nich jeśli weźmiemy 3 dowolne kolejne wyrazy ciągu to pierwszy wyraz pomnożony przez trzeci wyraz zawsze różni się od kwadratu wyrazu drugiego o 1
13,21,34
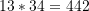
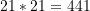
21,34,55
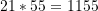
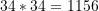
- Trzecia właściwość jest związana z wspomnianą wyżej liczbą fi jeżeli będziemy liczyć stosunki kolejnych liczb w ciągu będziemy dążyć do coraz dokładniejszej reprezentacji liczby fi
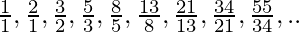 co daje nam
co daje nam
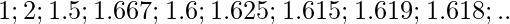
Obliczanie Ciągu iteracyjnie ( elementu na danej pozycji )
Do tego zadania napisałem taką o to małą funkcję w c++
unsigned long int calculateFibonacci( int index ){
unsigned long int lastNumber = 1;
unsigned long int sumReturn = 0;
unsigned long int tmpValue = 0;
for( int iPosition = 0 ; iPosition < index ; iPosition++ ){ tmpValue = sumReturn; sumReturn += lastNumber; lastNumber = tmpValue; } return sumReturn; } bardzo prosta i działającą całkiem dobrze. No właśnie całkiem ? czy da się to jakoś przyspieszyć ? Otóż da 😉
zaprzęgniemy do tego funkcje typu naked oraz trochę asm
http://gynvael.coldwind.pl/?id=14
Na początku sposób w jaki testowałem wydajność rozwiązań
int iLoop = 1000000;
SYSTEMTIME timeStart,
timeEnd;
GetSystemTime( &timeStart );
while( iLoop >= 0 ){
calculateFibonacci( 1000 );
iLoop--;
}
GetSystemTime( &timeEnd );
std::cout << "Time : " << ( ( timeEnd.wSecond * 1000 ) + timeEnd.wMilliseconds ) - ( ( timeStart.wSecond * 1000 ) + timeStart.wMilliseconds ) << std::endl; widać tutaj deklarowanie i incjalizacje zmiennej iLoop której wartość wynosi milion dalej tworzymy dwie struktury
SYSEMTIME
które służą do „przechowywania czasu”
następnie wywołujemy
GetSystemTime z windows.h dalej nasza funkcja obliczająca dany element ciągu zostaje wywołana 1000000 razy za każdym razem obliczając element na 1000 pozycji
Następnie mamy pobranie czasu oraz obliczenie delty i jej wyświetlenie. Taki sposób benchmarkingu daje niepewne wyniki i jest dość niedokładny ale jednak dla naszych domowych warunków wystarczy.
Jaki jest wynik ? Na moim komputerze oscyluje on około 3200
Znowu pada pytanie czy można to zoptymalizować i jak bardzo ?
Tak jak wcześniej wspomniałem posłużyłem się tutaj asm ( składnia intel czyli do parametrów kompilatora trzeba dodać -masm=intel )
extern "C"{
unsigned int calculateFibonacciASM( int index );
}
__asm(
".globl _calculateFibonacciASM\n"
"_calculateFibonacciASM:\n"
"mov ecx, dword ptr [ esp + 4 ] \n"
"mov eax,0\n"
"mov esi,1\n"
"mov edi,0\n"
"loop:\n"
"test ecx,ecx\n"
"jbe loopEnd\n"
"sub ecx,1\n"
"mov edi,eax\n"
"add eax,esi\n"
"mov esi,edi\n"
"jmp loop\n"
"loopEnd:\n"
"ret"
);
Widzimy tutaj deklaracje funkcji naked oraz jej etykietę wraz z kodem
Kod testów
iLoop = 1000000;
GetSystemTime( &timeStart );
while( iLoop >= 0 ){
calculateFibonacciASM( 1000 );
iLoop--;
}
GetSystemTime( &timeEnd );
std::cout << "Time : " << ( ( timeEnd.wSecond * 1000 ) + timeEnd.wMilliseconds ) - ( ( timeStart.wSecond * 1000 ) + timeStart.wMilliseconds ) << std::endl; Jakie są wyniki ? Na moim komputerze oscyluje on wokół 750. Czyli uzyskaliśmy wzrost wydajności o około 72-77% całkiem nieźle :). Pełen kod programu którego używałem do testowania
#include
#include
extern "C"{
unsigned int calculateFibonacciASM( int index );
}
__asm(
".globl _calculateFibonacciASM\n"
"_calculateFibonacciASM:\n"
"mov ecx, dword ptr [ esp + 4 ] \n"
"mov eax,0\n"
"mov esi,1\n"
"mov edi,0\n"
"loop:\n"
"test ecx,ecx\n"
"jbe loopEnd\n"
"sub ecx,1\n"
"mov edi,eax\n"
"add eax,esi\n"
"mov esi,edi\n"
"jmp loop\n"
"loopEnd:\n"
"ret"
);
unsigned long int calculateFibonacci( int index ){
unsigned long int lastNumber = 1;
unsigned long int sumReturn = 0;
unsigned long int tmpValue = 0;
for( int iPosition = 0 ; iPosition < index ; iPosition++ ){ tmpValue = sumReturn; sumReturn += lastNumber; lastNumber = tmpValue; } return sumReturn; } int main(){ int iLoop = 1000000; SYSTEMTIME timeStart, timeEnd; GetSystemTime( &timeStart ); while( iLoop >= 0 ){
calculateFibonacci( 1000 );
iLoop--;
}
GetSystemTime( &timeEnd );
std::cout << calculateFibonacci( 1000 ) << std::endl; std::cout << "Time : " << ( ( timeEnd.wSecond * 1000 ) + timeEnd.wMilliseconds ) - ( ( timeStart.wSecond * 1000 ) + timeStart.wMilliseconds ) << std::endl; iLoop = 1000000; GetSystemTime( &timeStart ); while( iLoop >= 0 ){
calculateFibonacciASM( 1000 );
iLoop--;
}
GetSystemTime( &timeEnd );
std::cout << calculateFibonacciASM( 1000 ) << std::endl; std::cout << "Time : " << ( ( timeEnd.wSecond * 1000 ) + timeEnd.wMilliseconds ) - ( ( timeStart.wSecond * 1000 ) + timeStart.wMilliseconds ) << std::endl; char ignoreInput; std::cin >> ignoreInput;
return 0;
}
Źródła
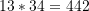
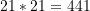
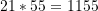
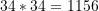
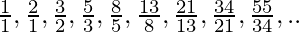 co daje nam
co daje nam
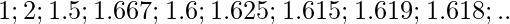
Używając składni AT&T mógłbyś zrobić tą funkcję ładniej ( czytelniej ) 😛
Oraz wydaje mi się że GetTickCount() było by w tym przypadku dokładniejsze.
Jestem przyzwyczajony do składni intela 😉