void vectorCreate( double fVecU[ 3 ] , double fVecV[ 3 ] , double fVecOut[ 3 ] ){
fVecOut[ 0 ] = ( fVecU[ 1 ] * fVecV[ 2 ] ) + ( fVecU[ 2 ] * fVecV[ 1 ] );
fVecOut[ 1 ] = ( - ( fVecU[ 0 ] * fVecV[ 2 ] ) ) - ( fVecU[ 2 ] * fVecV[ 0 ] );
fVecOut[ 2 ] = ( fVecU[ 0 ] * fVecV[ 1 ] ) + ( fVecU[ 1 ] * fVecV[ 0 ] );
}
Przykład użycia to wyznaczanie np. wektora normalnego ( prostopadłego do powierzchni )
Wyznaczanie wektora prostopadłego
Aby wyznaczyć wektor prostopadły potrzebujemy dwóch wektorów jeśli mieli byśmy tylko jeden to wektorów prostopadłych do niego jest nieskończenie wiele 😉
Wyznaczanie wektora prostopadłego można inaczej nazwać iloczynem wektorowym
Jak łatwo zauważyć mając dwa wektory możemy wyznaczyć dwa wektory prostopadłe do nich ( mające ten sam kierunek ale różne zwroty )
Wektory zwracany przez wzór poniżej to wektor którego kierunek możemy wyznaczyć regułą prawej dłoni
Dwa wektory które mamy oznaczyłem jako U i V wektory wynikowy jako W
Wzór to
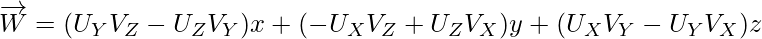 Funkcja w C++
Funkcja w C++
wydaje mi się że poprawnie powinno wyglądać to tak:
void vectorCreate( double fVecU[ 3 ] , double fVecV[ 3 ] , double fVecOut[ 3 ] ){
fVecOut[ 0 ] = ( fVecU[ 1 ] * fVecV[ 2 ] ) – ( fVecU[ 2 ] * fVecV[ 1 ] );
fVecOut[ 1 ] = -( ( fVecU[ 0 ] * fVecV[ 2 ] ) – ( fVecU[ 2 ] * fVecV[ 0 ] ) );
fVecOut[ 2 ] = ( fVecU[ 0 ] * fVecV[ 1 ] ) – ( fVecU[ 1 ] * fVecV[ 0 ] );
}
Tutaj załączam filmik, gdzie jest to w miarę wytłumaczone: https://www.youtube.com/watch?v=HcaruZZ0jz4
Ogólnie używam tego wzoru do ustalenia wektora normalnego powierzchni, ponieważ od niego zależy jak będzie na powierzchnię „padało światło”. Tutaj podaję jaki jaki jest wynik: https://ibb.co/f0zz6MY